BFS 란 단어 뜻 그대로 깊이 우선 탐색이라는 뜻이다.
DFS와 구현방법은 비슷하지만 결과는 확연히 다르다.
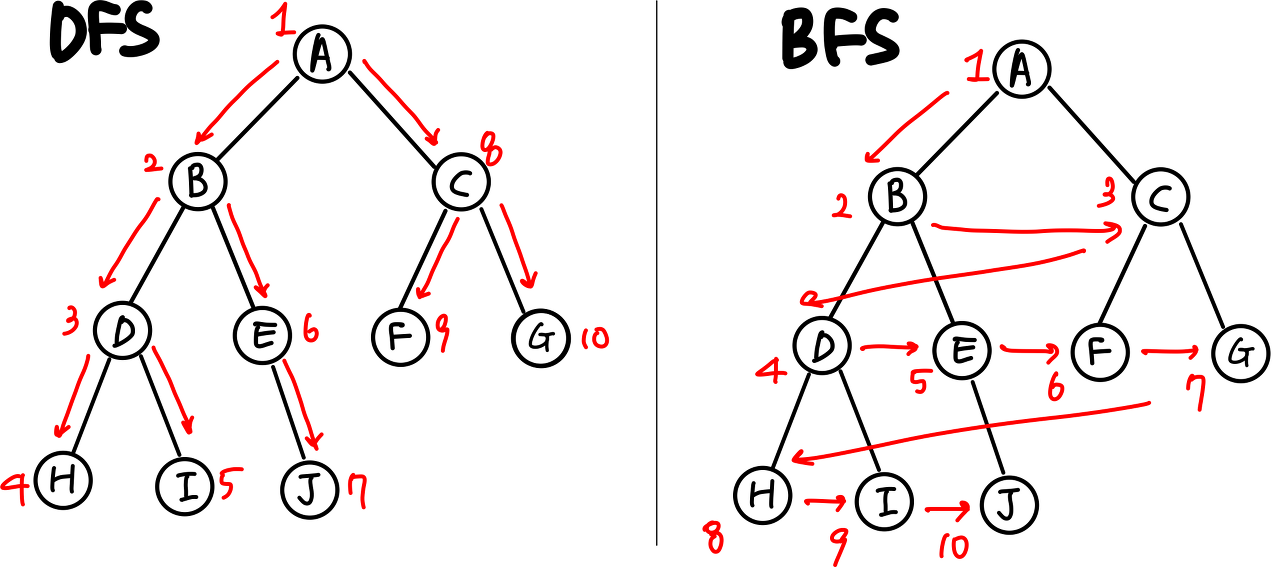
마찬가지로 BFS를 구하기 위해 필요한 정보부터 알아보자.
① 전에 방문한 정점(vertex)을 알아야 한다. 따라서 각 정점(vertex)의 방문 여부를 저장하는 자료구조가 필요핟.
- 한번 방문한 정점(vertex)이라면 들릴 필요가 없다.
이 BFS는 DFS보다 간단하게 구현이 가능하다.
Queue 자료구조 를 사용한다.
[ Queue 이용한 BFS 구현 ]
입력으로 인접 리스트 형태의 그래프가 주어졌을때
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
vector<vector<int>> adjacent{ 9 };
vector<bool> visited(9,false);
queue<int> q;
void BFS(int start) {
q.push(start);
cout << "Visit : " << start << endl;
visited[start] = true;
while (!q.empty()) {
auto next = q.front();
q.pop();
for (int i = 0; i < adjacent[next].size(); i++) {
if (!visited[adjacent[next][i]]) {
q.push(adjacent[next][i]);
cout << "Visit : " << adjacent[next][i] << endl;
visited[adjacent[next][i]] = true;
}
}
}
}
void initMarks() {
for (auto elem : visited) {
elem = false;
}
}
void BFS() {
BFS(0);
}
bool search(int start, int end) { // 엔지니어 대한민국(유튜브) 'Graph에서 두지점의 경로 찾기'
initMarks();
queue<int> temp;
temp.push(start);
visited[start] = true;
while (!temp.empty()) {
int next = temp.front();
temp.pop();
if (next == end) return true;
for (int elem : adjacent[next]) {
if (!visited[elem]) {
temp.push(elem);
visited[elem] = true;
}
}
}
return false;
}
DFS보다 간단하기 때문에 딱히 주의해야할점은 없다.
다만 BFS는 최단 경로 문제에 자주 사용된다. ( 이 부분은 다익스트라 파트에서 다시 보자.)
+ 경로를 출력하는 법도 알아야한다 - ( 재귀 or 스택 ) 이용.
구글링 하다 전형적인 BFS 문제를 풀어 보았다.
<문제>
1부터 n(n은 10000이하) 까지 번호로 이름이 붙여진 정점이 있습니다. 정점들을 간선들로 연결되어 있습니다. 간선을 통해 임의의 정점에서 연결된 정점으로 이동할때 거리가 1씩 증가합니다. 시작점에서 다른 모든 정점들까지 최단거리를 구하세요.
<입력 정보>
첫줄에 n m k 가 한칸씩 공백으로 분리되어 주어집니다.
1) n은 정점의 개수 입니다. 1부터 n까지 n개의 정점이 존재합니다. (1 <= n <= 1만)
2) m은 간선의 개수 입니다. (1 <= m <= 1만)
3) k는 시작점의 번호입니다.
둘째줄부터 m개의 줄에 간선의 정보가 주어집니다. 간선의 정보는 두개의 정수 a b로 표현됩니다. (a와 b는 간선으로 연결되어 있다.)
<출력 방법>
1~n번까지 각 정점에 대해 최단 거리를 출력하세요.(한 줄씩 줄 바꿈 해서) 단, 방문할 수 없는 정점에 대해서는 -1을 출력하세요
[ 정답 코드 보기 ]
#include<iostream>
#include<queue>
#include<vector>
using std::cin;
using std::cout;
int n, m, k;
int a, b;
std::vector<std::vector<int>> adjacent{ 10001, };
int visited[10001];
std::queue<int> que;
void Bfs(int start) {
que.push(start);
visited[start]++;
while (!que.empty()) {
int current = que.front();
que.pop();
for (int i = 0; i < adjacent[current].size(); i++) {
int next = adjacent[current][i];
if (visited[next]==-1) {
que.push(next);
visited[next] = visited[current] + 1;
}
}
}
}
int main() {
cin >> n >> m >> k;
std::fill_n(visited, n + 1, -1);
for (int i = 1; i <= m; i++) {
cin >> a >> b;
adjacent[a].push_back(b);
adjacent[b].push_back(a);
}
Bfs(k);
for (int i = 1; i <= n; i++) {
cout << visited[i] << '\n';
}
return 0;
}
최단 거리를 저장하는 배열을 따로 만들지 말고, visited를 bool 타입이 아니라 int 타입으로 만들고 방문할 때마다
visited [ 방문 노드 ] = visited [ 전 노드 ] + 1 ;
해주는 방법을 생각할 수 있어야한다.
위의 문제를 출력만 다르게 해서 다시 풀어 보자.
힌트는
from[ ] 배열을 이용해서 이전 노드를 저장.
<출력 >
위의 k번째 노드를 시작으로 입력 노드 번호 t 가 주어졌을때, 시작점 k 에서 해당 정점 t 까지 도달하는데 거치는 정점을 공백으로 분리해서 출력하세요.
단, 방문할 수 없는 정점에 대해서는 -1을 출력하세요.
그리고, 시작점은 시작점 하나만 출력하세요
뭔가를 거꾸로 할때는 스택을 이용한다!!
재귀도 좋다. 재귀는 내부적으로 스택으로 이루어져 있기 때문에!!
reference : https://velog.io/@skyepodium/BFS%EB%8A%94-%EB%82%AF%EC%84%A4%EC%96%B4%EC%84%9C
'CS > Algorithm' 카테고리의 다른 글
| 최단 경로 ② ( Floyd - Warshall ) (0) | 2021.11.17 |
|---|---|
| 최단 경로 & 그래프 문제 유형 (0) | 2021.11.17 |
| Kruskal ( Union - Find ) (0) | 2021.11.12 |
| MST ( Minimum Spanning Tree ) - Kruskal , Prim (0) | 2021.11.11 |
| DFS ( Depth First Search ) (0) | 2021.11.10 |